Solving Einstein riddle with Z3

Einstein’s five-houses consists, as the title says, of 5 houses. Each house has a certain color. Inside of each house, its owner has a pet, smokes a certain brand of cigars, drinks a certain beverage, and has a nationality. Any of these is unique between the house owners.

For a more detailed explanation, here is one from the University of Delaware.

Hints

The riddle gives the following hints:

• the Brit lives in the red house
• the Swede keeps dogs as pets
• the Dane drinks tea
• the green house is on the left of the white house
• the green house’s owner drinks coffee
• the person who smokes Pall Mall rears birds
• the owner of the yellow house smokes Dunhill
• the man living in the center house drinks milk
• the Norwegian lives in the first house
• the man who smokes blends lives next to the one who keeps cats
• the man who keeps horses lives next to the man who smokes Dunhill
• the owner who smokes BlueMaster drinks beer
• the German smokes Prince
• the Norwegian lives next to the blue house
• the man who smokes blend has a neighbor who drinks water

Question

Given these hints, you have to answer the question Who owns the fish?

Solving it with Python Z3

To solve this problem I decided to try Microsoft’s Z3 Theorem Prover. It can be used in different programming languages such as C, C++, Java, Julia, Python among others. I decided to go with the Python interface.

Z3 can be used to solve Satisfiability Modulo Theories (SMT) problems. In simple terms, these problems involve several variables and logical relationships between them. The solver will try to find, if possible, a set of values for the variables that satisfy the relationships.

Implementation

For simplicity, I have assigned each house with a letter: A, B, C, D, E. Then, I created five 5x5 matrices. Each matrix corresponds to a category: Color, Nationality, Drink, Cigar, Pet. Inside each matrix, the rows correspond to the different values the category could take. For example, in the Color matrix, the rows correspond to Red, Blue, Green, Yellow, White. The columns identify each house: A, B, C, D, E.

Inside the cell of each matrix, I have assigned a Z3 Boolean value. It will be true or 1 if, for the corresponding category, the house has a certain value. For example, if house A is of color red, in the Color matrix the cell corresponding to column A and row red will contain a true or 1. Logically, the rest of the values will contain false or 0

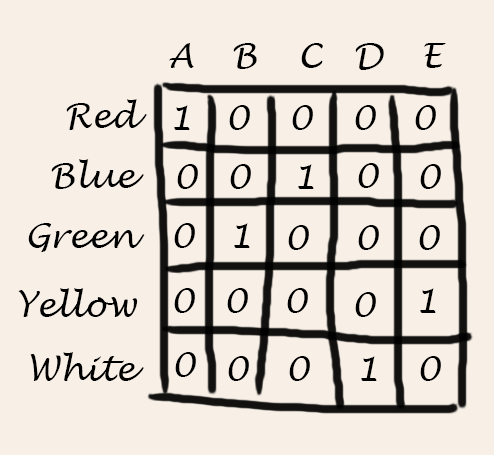
An important property is that each row or column can only contain a 1 or true value. It isn’t possible that, for example, both the A and C houses share a color. It is also impossible that a house has two different colors.

This is an important property and it will be a logical restraint of our Z3 model.

Let’s see how I implemented it in Python.

from z3 import *

houses = ["A", "B", "C", "D", "E"]
names = {"Color": ["Red", "Blue", "Green", "Yellow", "White"],
        "Nationality": ["Brit", "Swede", "Dane", "Norwegian", "German"],
        "Drink": ["Coffee", "Milk", "Beer", "Water", "Tea"],
        "Cigar": ["PallMall", "Dunhill", "Prince", "BlueMaster", "Blends"],
        "Pet": ["Dog", "Bird", "Cat", "Fish", "Horse"]}

matrices = {}

def add_names_constraints(solver, names):
    for (name, values) in names.items():
        amount_items = len(values)
        matrix = [[0 for x in range(amount_items)] for y in range(amount_items)]
        for i in range(amount_items):
            for j in range(amount_items):
                matrix[i][j] = Bool("{}_{}".format(houses[j], values[i]))

        for i in range(amount_items):
            solver.add(Sum([If(item, 1, 0) for item in matrix[i]]) == 1)
            solver.add(Sum([If(row[i], 1, 0) for row in matrix]) == 1)

        matrices[name] = matrix

First I defined the houses’ names and all of the categories and their possible values.

Then, I created the function add_names_constraints that has two purposes:

• To create the five matrices and populate them with Booleans values (lines 17 to 20).
• To create the Z3 model constraints corresponding to each matrix row and column (lines 22 to 24).

Basic relationships

Now, let’s continue establishing model relationships. The riddle gives us a lot of basic relationships. These take two different values from different categories and assign them to a certain person or house. The basic relationships are:

• the Brit lives in the red house
• the Swede keeps dogs as pets
• the Dane drinks tea
• the green house’s owner drinks coffee
• the person who smokes Pall Mall rears birds
• the owner of the yellow house smokes Dunhill
• the owner who smokes BlueMaster drinks beer
• the German smokes Prince

Here is the function that will be used to create these relationships.

def add_relation(solver, first_category, first_value,
                second_category, second_value):
    index1 = names[first_category].index(first_value)
    index2 = names[second_category].index(second_value)

    row1 = matrices[first_category][index1]
    row2 = matrices[second_category][index2]

    solver.add(Or([And(row1[i], row2[i]) for i in range(len(row1))]))

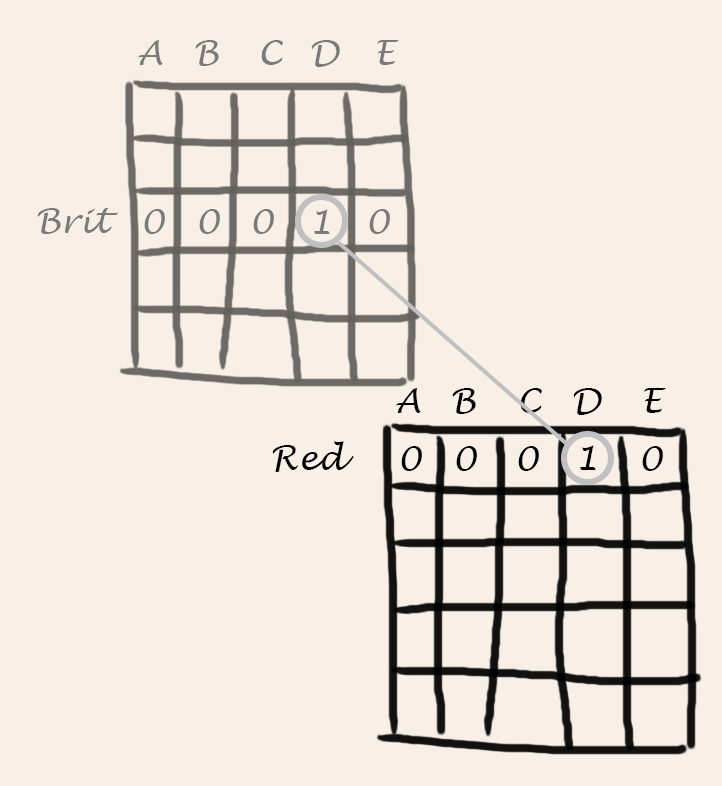
First, it transforms the text category and values into their corresponding indexes. Then it makes that the two rows have at least a coincidence in their corresponding house.

For example, the first relationship says: the Brit lives in the red house. That means that the Brit row in the nationalities matrix must be equal to the red row in the colors matrix.

As the code shows this relationship could be easily achieved with an And and an Or clauses.

House constraints

Next, we have the house constraints. These are simple to add to the model. The two house constraints that we have are:

• the man living in the center house drinks milk
• the Norwegian lives in the first house

def add_house_constraint(solver, house, category, value):
    index1 = names[category].index(value)
    index2 = houses.index(house)

    item = matrices[category][index1][index2]

    solver.add(item == True)

We simple force the corresponding cell to be true.

Neighbor constraints

Finally, we have the neighbor constraints. These come in the form of X lives next to Y. The riddle lists the following ones:

• the Norwegian lives next to the blue house
• the man who smokes blends lives next to the one who keeps cats
• the man who keeps horses lives next to the man who smokes Dunhill
• the man who smokes blend has a neighbor who drinks water
• the green house is on the left of the white house

This is the function that i came up with:

def add_neighbor_constraint(solver, first_category, first_value, 
                        second_category, second_value, left_only=False):
    index1 = names[first_category].index(first_value)
    index2 = names[second_category].index(second_value)

    row1 = matrices[first_category][index1]
    row2 = matrices[second_category][index2]

    conditions_list = [And(row1[i - 1], row2[i]) for i in range(1, len(row1))]
    if not left_only:
        conditions_list += [And(row2[i - 1], row1[i]) for i in range(1, len(row1))]

    solver.add(Or(conditions_list))

This function is the most complex, but its logic is very similar to the basic relationships. The only difference is that we keep a shift of \(\pm\)1 between the rows’ indexes.

We have a left_only clause that is by default False. For the last constraint the green house is on the left of the white house we put this value as True.

Final steps and result

We finished with all the logic of the model, we only need to call the functions to build the model.

s = Solver()

add_names_constraints(s, names)

add_relation(s, "Nationality", "Brit", "Color", "Red")
add_relation(s, "Nationality", "Swede", "Pet", "Dog")
add_relation(s, "Nationality", "Dane", "Drink", "Tea")
add_relation(s, "Color", "Green", "Drink", "Coffee")
add_relation(s, "Cigar", "PallMall", "Pet", "Bird")
add_relation(s, "Color", "Yellow", "Cigar", "Dunhill")
add_relation(s, "Cigar", "BlueMaster", "Drink", "Beer")
add_relation(s, "Nationality", "German", "Cigar", "Prince")

add_house_constraint(s, "C", "Drink", "Milk")
add_house_constraint(s, "A", "Nationality", "Norwegian")

add_neighbor_constraint(s, "Cigar", "Blends", "Pet", "Cat")
add_neighbor_constraint(s, "Cigar", "Dunhill", "Pet", "Horse")
add_neighbor_constraint(s, "Cigar", "Blends", "Drink", "Water")
add_neighbor_constraint(s, "Nationality", "Norwegian", "Color", "Blue")

add_neighbor_constraint(s, "Color", "Green", "Color", "White", left_only=True)

print (s.check())
print (s.model())

m = s.model()
true_statements = []

for x in m:
    if is_true(m[x]):
        true_statements.append(x.name())

result = {}

for house in houses:
    result[house] = [true_statements[i][2:] for i in range(len(true_statements))
                    if true_statements[i][0] == house]

print(result)

We added some prints to see the viability of the model and the model itself. In the end, we added some logic to parse the results. We would only like to see which values in the matrices contain a true value.

After running the program it shows us:

{'A': ['Dunhill', 'Cat', 'Yellow', 'Water', 'Norwegian'],
'B': ['Blue', 'Dane', 'Blends', 'Tea', 'Horse'],
'C': ['Bird', 'Brit', 'Red', 'PallMall', 'Milk'],
'D': ['Prince', 'German', 'Fish', 'Green', 'Coffee'],
'E': ['Dog', 'Beer', 'Swede', 'White', 'BlueMaster']}

We could see that the German is the owner of the fish.

Looking at the solution, we verify that our model worked correctly.