Min-cut problem variations

Last week I needed to solve a variation of the min-cut problem for flow networks. For those who don’t know about the minimum cut of a flow network, I will give a brief explanation.

Flow networks

A flow network is a directed graph, typically used to represent situations like traffic in computer networks, fluid in pipes, currents in an electrical circuit, vehicles in a road network.

This graph’s edges typically have an associated weight known as capacity. In simple terms, its defines the maximum flow that could pass by that edge.

Another important feature of these types of graphs is that they have a source node and a sink node. The source has only outgoing flow and the sink had only incoming flow.

As an example:

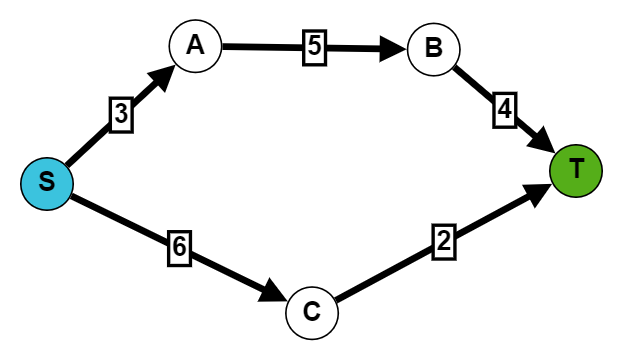
In this flow network, the S node is the source and the T node is the sink. The numbers along the edges represent the capacities. This is a pretty simple network, we obviously could represent much more complex ones.

Minimum cut problem

The minimum cut problem consists of, given a flow network, dividing it into two parts by cutting some edges. In one of the parts it must be included the source node and, in the other one, the sink node. It is a minimum cut because you have to select the edges which summation is minimum between all the possible cuts.

Following the previous example, I marked some possible cuts. In this case the minimum cut is the one in blue which takes the edges S-A and C-T, totaling a minimum of 5.

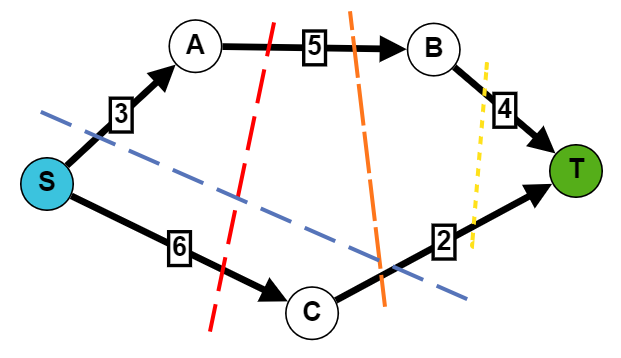
As a side note, the minimum cut is always the same as the maximum flow of the network, in this case 5.

Minimum cut with minimum edges problem

The classical minimum cut problem could be easily solved by algorithms like Ford-Fulkerson or Edmonds–Karp. But let’s analyze a special case of this problem.

Suppose we have a pipe system and we want to determine the minimum cut for making some reparations. As the reparations include changing some pipes, we would like, if possible, to replace the least amount of pipes.

For example, in the following network, we could find two minimum cuts: one consisting of two edges: S-A and C-B, and the other one consisting of only one: B-T. In both cases the flow is 3, the minimum possible. Running a typical algorithm like Ford-Fulkerson or Edmonds-Karp could give us any of the two possible solutions.

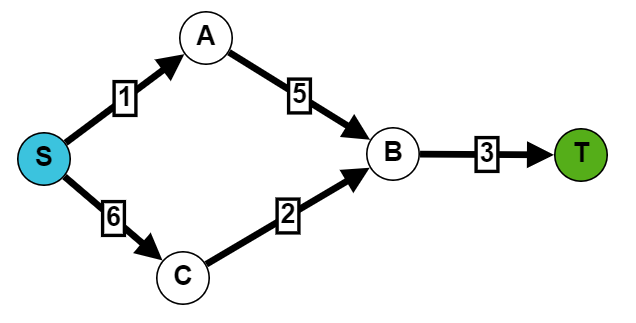
There is a simple but effective solution to this problem. You have to transform the network capacities by the following formula:

\[C' = C (|E| + 1) + 1\]

With \(C'\) the new capacity of each edge, \(C\) the old capacity, and \(\vert E \vert\) the amount of edges in the network.

Let’s look to our example with the updated capacities:

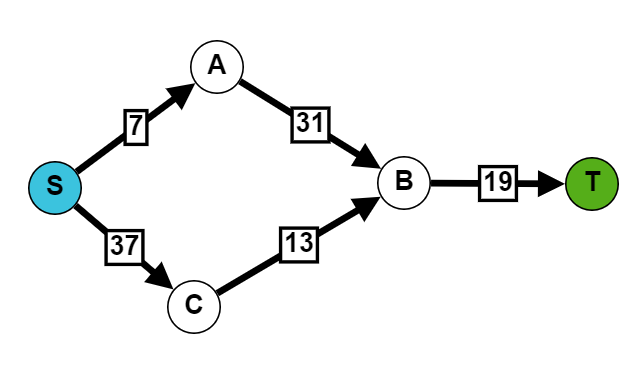
Our previous minimum cut of S-A and C-B now has a total capacity of 20. Simultaneously the B-T cut has a capacity of 19. A new and lonely minimum!

Why this formula works

Here I will detail a mathematical proof of why this formula works.

We would like to prove two things:

• Our formula doesn’t convert original non-minimum cuts to minimum cuts.
• From all the original minimum cuts, the formula keeps the one with the fewer amount of edges the strict minimum.

First proof

From the original network, let’s consider the minimum cut has a capacity \(k\) and cuts \(n\) edges. In our transformed network this cut will have a total capacity of \(k(|E| + 1) + n\). This is because:

\[\sum_{i=0}^n C_i(|E| + 1) + 1 =\]

\[= [C_0(|E| + 1) + 1] + [C_1(|E| + 1) + 1] + ... + [C_n(|E| + 1) + 1] =\]

\[= ((C_0 + C_1 + ... + C_n) (|E| + 1)) + n =\]

\[= k (|E| + 1) + n\]

Let us now take a non-minimal cut from the original network. It must have a capacity of at least \(k + 1\). Following the same reasoning as before, this cut will have a capacity of \((k + 1)(|E| + 1) + m\) with \(m\) the edges that this cut crosses.

Let us compare the two cuts in the transformed network:

\[(k + 1)(|E| + 1) + m =\]

\[= k (|E| + 1) + (|E| + 1) + m >\]

\[> k (|E| + 1) + n + m >\]

\[> k (|E| + 1) + n\]

We can say that \((\vert E \vert + 1) > n\) because \(n\), the number of edges in any cut, is, at most, equal to the number of edges \(\vert E \vert\) in the graph.

Second proof

Let us consider we have a graph with two (or more) minimal cuts. First, we will consider the one that crosses fewer edges. Again we will define a capacity of \(k\) and that crosses \(n\) edges. Also, we will define another minimal cut of, logically, capacity \(k\) but with more edges: \(n + u\) with \(u\) a natural number.

Following the procedures in the first proof, we could easily conclude that the new capacities of the cuts in the transformed graph will be: \(k(\vert E \vert + 1) + n\) and \(k(\vert E \vert + 1) + (n + u)\). The minimal cut with minimal edges from the original graph will be the strict minimal in the new graph.

Minimum cut with maximum edges problem

Now, let’s consider the opposite problem. We want to find the minimum cut that contains the maximum amount of edges. Like before we could transform the edges’ values by a simple formula:

\[C' = C |E| - 1\]

Again I will show that this formula doesn’t convert non-minimal cuts to minimal cuts and that the minimal cut with maximum amount of edges is the new strict minimal cut.

First proof

Like before, we could take two cuts: a minimal cut that crosses \(n\) edges and has a capacity \(k\) and a non-minimal cut that crosses \(m\) edges and has a capacity of at least \(k + 1\).

After applying the proposed transformation, the minimal cut will have a capacity of \(k \vert E \vert - n\):

\[\sum_{i=0}^n C_i |E| - 1 =\]

\[= (C_0 |E| - 1) + (C_1 |E| - 1) + ... + (C_n |E| - 1) =\]

\[= ((C_0 + C_1 + ... + C_n) |E|) - n =\]

\[= k |E| - n\]

With the same reasoning, the transformed capacity of our non-minimal cut will be \((k + 1) \vert E \vert - m\).

So let’s compare the two of them:

\[k \vert E \vert - n =\]

\[= k |E| - n + m - m =\]

\[= k |E| + (m - n) - m <\]

\[< k |E| + |E| - m =\]

\[= (k + 1) \vert E \vert - m\]

In the third and fourth lines we considered that the difference of two numbers indicating amounts of edges \(n\), \(m\) must always be less than the total amount of edges \(\vert E \vert\).

Second proof

As done before we will consider two cuts of the same capacity \(k\). One of them will cross \(n\) edges and the other \(n + u\) edges. In the transformed graph we would like that the second one to become the strict minimum cut.

This is very simple to prove. The capacities in the transformed graph will be \(k \vert E \vert - n\) and \(k \vert E \vert - n - u\). Clearly, the second one will be the new minimum cut.

A look at the new graph

Let’s see how the simple graph we have been working on would look like in this minimum cut with maximum edges case:

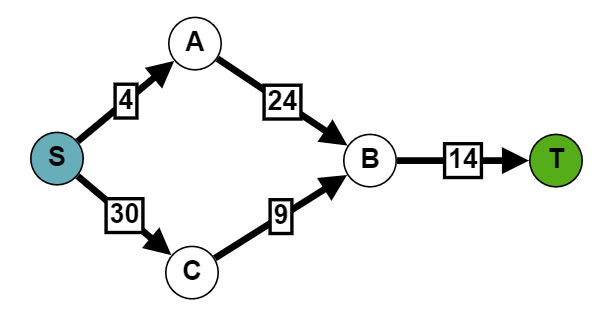
The cut consisting of S-A and C-B has a capacity of 13 while the cut of B-T has a capacity of 14. We have a new minimum!

Final thoughts

The shown methods work with positive integer and positive non-integer numbers. Still, it has the benefit of keeping integer weights to new integer weights.

Another approach in the same style as the ones shown is to do the simpler transformation of:

\[C' = C \pm \epsilon\]

Taking \(C' = C + \epsilon\) for the minimal edges case and \(C' = C - \epsilon\) for the maximum edges case. For this transformation to work we have to take a small \(\epsilon\) in comparison to \(1 / \vert E \vert\). This new method has the clear disadvantage of introducing non-integers weights.